中学生 勉強なんて 怖くない
~ 勉強が苦手な中学生のために ~
- TOP
- >
- 中学3年 数学 練習問題一覧
- >
- 放物線と直線
勉強しないで後悔するくらいなら、
後悔してもいいから、勉強しよう。
勉強すれば、必ず力になる。
勉強すれば、必ず自分のためになる。
勉強すれば、後悔なんてしない。
~ 中学3年 数学 ~
Lesson 27 放物線と直線
第4章 xの2乗に比例する関数
<前:L26- 変化の割合 の問題 L27- 放物線と直線 の解答:次>
【練習問題1】
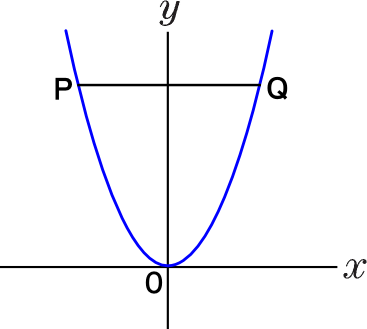
関数y=x2のグラフと直線y=4の交点をP,Qとする。
このとき、点P,Qの座標を求めなさい。
ただし、点Pのx座標は点Qのx座標より大きいものとする。
【練習問題2】
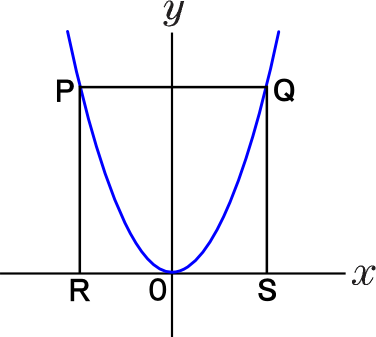
右図のように、関数y=ax2のグラフと直線y=27の交点をP,Qとする。
PQ=18のとき、aの値を求めなさい。
【練習問題3】
右図のように、関数y=12x2のグラフ上に点P,Qを、x軸上に点R,Sをとる。
四角形PRSQが正方形となるとき、点Qの座標を求めなさい。
【練習問題4】
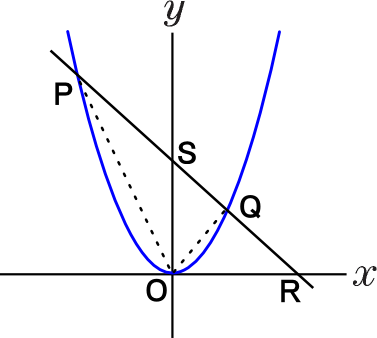
右図のように、関数y=x2のグラフ上に点P,Qがある。
点P,Qを通る直線とx軸,y軸との交点をそれぞれR,Sとする。
点P,Qのx座標がそれぞれx=-5,x=3のとき以下の質問に答えなさい。
[1] 点P,Qの座標を求めなさい。
[2] 直線PQの式を求めなさい。
[3] 点R,Sの座標を求めなさい。
[4] △OPQの面積を求めなさい。(座標軸の1目盛りを1cmとする)
[5] PQを対角線とする平行四辺形POQTをつくるとき、点Tの座標を求めなさい。
【練習問題5】
放物線と直線が点P(-4,m)と点Q(2,-6)で交わっている。
このとき、以下の質問に答えなさい。
[1] 放物線の式を求めなさい。
[2] mの値を求めなさい。
[3] 直線の式を求めなさい。
【練習問題6】
放物線と直線が点P,Qで交わっていて、直線PQとy軸との交点を点Rとする。
点P(-3,6),点R(0,12)のとき、点Qの座標を求めなさい。
<前:L26- 変化の割合 の問題 L27- 放物線と直線 の解答:次>
中1数学・練習問題一覧 中2数学・練習問題一覧 中3数学・練習問題一覧
