中学生 勉強なんて 怖くない
~ 勉強が苦手な中学生のために ~
- TOP
- >
- 中学2年 数学 練習問題一覧
- >
- 『 第5章 図形と合同 』 の復習テスト
勉強しないで後悔するくらいなら、
後悔してもいいから、勉強しよう。
勉強すれば、必ず力になる。
勉強すれば、必ず自分のためになる。
勉強すれば、後悔なんてしない。
~ 中学2年 数学 ~
『 第5章 図形と合同 』 の復習テスト
第5章 図形と合同
<前:L41- 平行線と面積 の問題 『 第5章 図形と合同 』 の復習テスト の解答:次>
【練習問題1】 ( 参照 : Lesson34 Lesson38 )
∠xの大きさを求めなさい。
ただし、[2],[4],[5],[6]の四角形は平行四辺形とする。
[1]

[3]
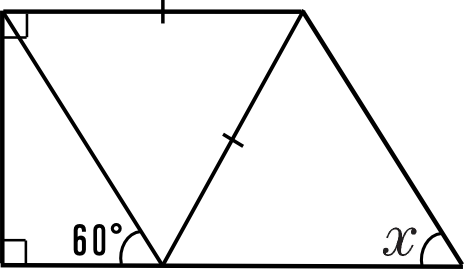
[5]

[2]

[4]

[6]

【練習問題2】 ( 参照 : Lesson41 )
以下の質問に答えなさい。

[1] 右図の平行四辺形ABC Dの面積は26cm2である。
辺CD上に点Pをとったとき、△ABPの面積を求めなさい。

[2] 右図の平行四辺形ABC Dの面積は100cm2である。
点Pを辺ADの中点に、点Qを辺BC上にとる。
このとき、△AQPの面積を求めなさい。
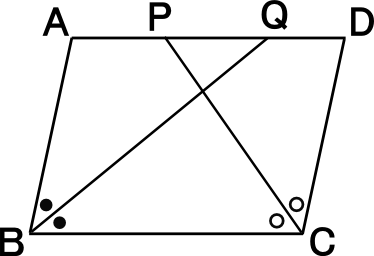
[3] 右図の平行四辺形ABC Dで、∠B,∠Cの二等分線と辺ABとの交点を
それぞれ、P,Qとする。
AB=10cm,BC=14cmのとき、PQの長さを求めなさい。
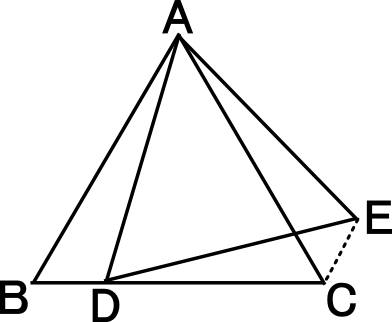
【練習問題3】 ( 参照 : Lesson34 Lesson35 Lesson37 )
右図の△ABCと△ADEは正三角形である。
このとき、BD=CEであることを証明しなさい。
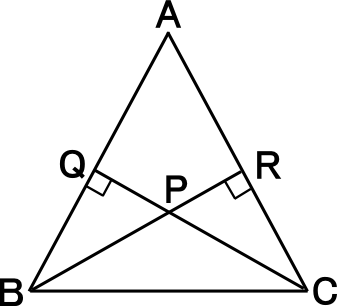
【練習問題4】 ( 参照 : Lesson34 Lesson35 Lesson36 Lesson37 )
右図の三角ABC において、点B,Cから辺AC,ABにそれぞを垂線をひき、その交点をPとする。
BQ=CRのとき、以下の証明をしなさい。
[1] △PBCは二等辺三角形である
[2] △ABCは二等辺三角形である
[3] △PQB≡△PRC
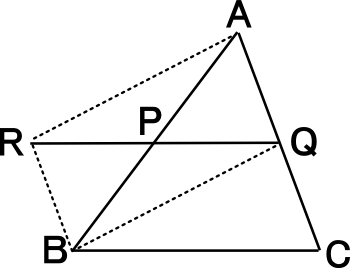
【練習問題5】 ( 参照 : Lesson38 Lesson39 Lesson40 )
右図のように、△ABCの辺AB,ACに中点P,Qをとる。
QPの延長線上にPQ=PRとなるように点Rをとって、四角形ARBQをつくった。
このとき四角形ARBQが平行四辺形であることを証明しなさい。
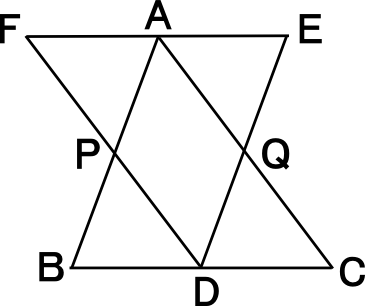
【練習問題6】 ( 参照 : Lesson38 Lesson39 Lesson40 )
右図において、△ABC≡△DEFで、FE∥BCである。
このとき、四角形APDQが平行四辺形であることを証明しなさい。
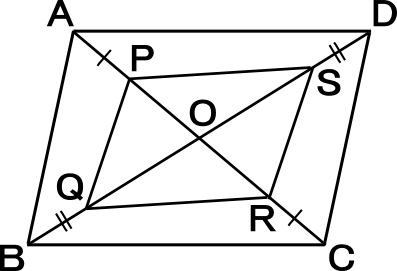
【練習問題7】 ( 参照 : Lesson38 Lesson39 Lesson40 )
右図のように、平行四辺形ABCDの対角線の交点をOとする。
また、AC上に点P,Rを、対角線BD上に点Q,Sを、AP=CR,BQ=DSとなるようにとる。
このとき四角形PQRSは平行四辺形であることを証明しなさい。
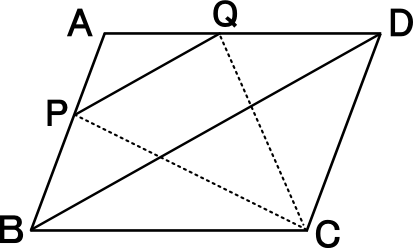
【練習問題8】 ( 参照 : Lesson41 )
右図の平行四辺形ABCDの対角線BDに平行な線をひき、辺AB,ADとの交点をそれぞれP,Qとする。
このとき、△PBC=△QCDであることを証明しなさい。
<前:L41- 平行線と面積 の問題 『 第5章 図形と合同 』 の復習テスト の解答:次>
中1数学・練習問題一覧 中2数学・練習問題一覧 中3数学・練習問題一覧
