中学生 勉強なんて 怖くない
~ 勉強が苦手な中学生のために ~
- TOP
- >
- 中学3年 数学 練習問題一覧
- >
- 中点連結定理
勉強しないで後悔するくらいなら、
後悔してもいいから、勉強しよう。
勉強すれば、必ず力になる。
勉強すれば、必ず自分のためになる。
勉強すれば、後悔なんてしない。
~ 中学3年 数学 ~
Lesson 34 中点連結定理
第5章 図形と相似
<前:L33- 三角形の比 の問題 L34- 中点連結定理 の解答:次>
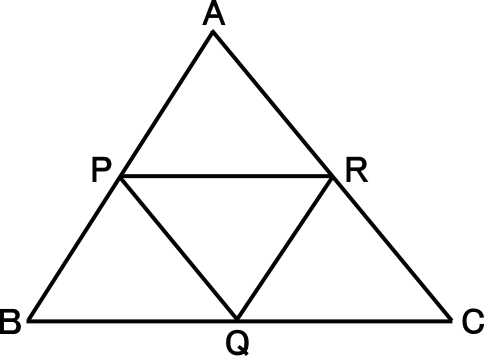
【練習問題1】
右図の△ABCの辺AB,BC,CAのそれぞれの中点をP,Q,Rとする。
このとき、以下の質問に答えなさい。
[1] △ABC∽△QRPを証明しなさい。
[2] PR=3cmのとき、BCの長さを求めなさい。
[3] AC=7cmのとき、PQの長さを求めなさい。
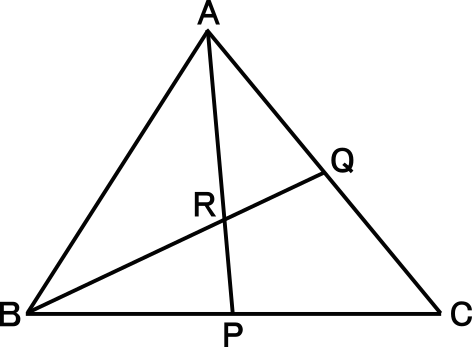
【練習問題2】
右図の△ABCの2点P,Qは、それぞれ辺BC,CAの中点で、点Rは線分AP,BQの交点である。
BQ=15cmのとき、RQの長さを求めなさい。
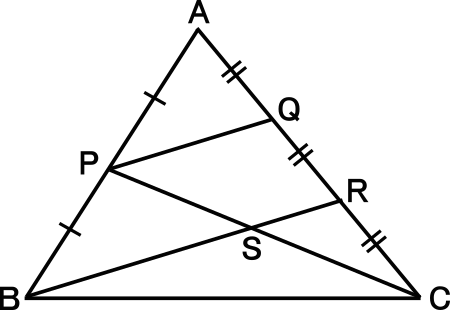
【練習問題3】
右図の△ABCにおいて、点Pは辺ABの中点、2点Q,Rは辺ACを3等分する点、点SはBRとCPの交点である。
PQ=5cmのとき、BSの長さを求めなさい。
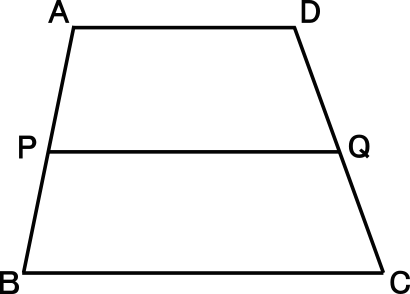
【練習問題4】
右図の四角形ABCDは、AD∥BCの台形で、2点P,Qはそれぞれ辺AB,DCの中点である。
AD=14cm,BC=22cmのとき、PQの長さを求めなさい。
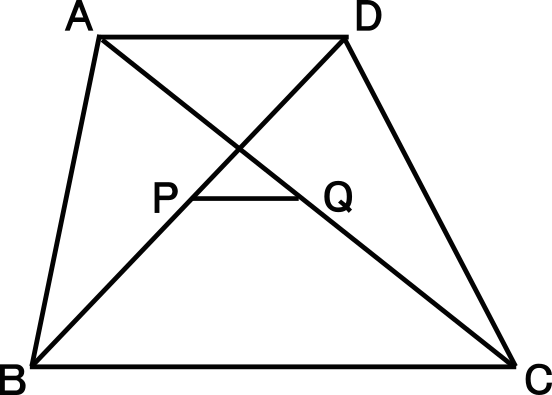
【練習問題5】
右図の四角形ABCDは、AD∥BCの台形で、2点P,Qはそれぞれ対角線AC,DBの中点である。
AD=10cm,BC=19cmのとき、PQの長さを求めなさい。
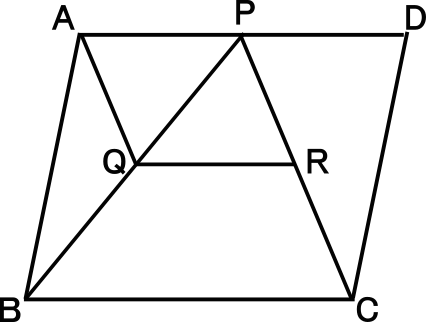
【練習問題6】
右図の平行四辺形ABCDで、点Pは辺ABの中点で、2点Q,RはそれぞれBP,CPの中点である。
このとき、四角形AQRPが平行四辺形になることを証明しなさい。
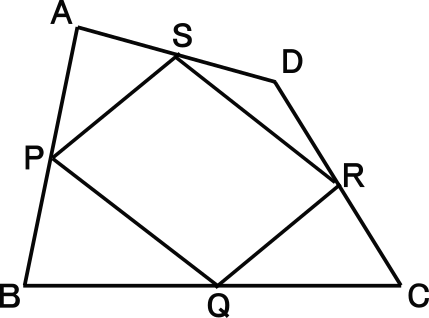
【練習問題7】
右図の四角形ABCDで、4辺AB,BC,CD,DAの中点をそれぞれ、P,Q,R,Sとする。
このとき、四角形PQRSが平行四辺形になることを証明しなさい。
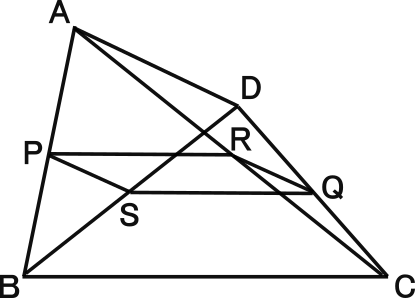
【練習問題8】
右図の四角形ABCDにおいて、2点P,Qはそれぞれ辺AB,DCの中点で、2点R,Sはそれぞれ辺AC,BDの中点である。
このとき、四角形PSQRが平行四辺形になることを証明しなさい。
<前:L33- 三角形の比 の問題 L34- 中点連結定理 の解答:次>
中1数学・練習問題一覧 中2数学・練習問題一覧 中3数学・練習問題一覧
