中学１年数学練習問題　切り取った立体の体積の求め方と解答

ＴＯＰ
＞
中学１年　数学　練習問題一覧
＞
切り取った立体の体積

勉強しないで後悔するくらいなら、
後悔してもいいから、勉強しよう。
勉強すれば、必ず力になる。
勉強すれば、必ず自分のためになる。
勉強すれば、後悔なんてしない。

～　中学１年　数学　～

Lesson 45　　　　　切り取った立体の体積

第６章　空間図形

＜＜　Ｌ４５ - 切り取った立体の体積の解答消去　　『第６章　空間図形』の復習テストの問題に進む　＞＞

【練習問題１】
右図の［１］［２］は、立方体をある平面で切り取って、その切り口に色をつけたものです。
このとき、以下の問いに答えなさい。

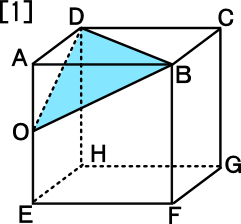
$立方体の切り口$

［１］　２点Ｂ，Ｄと辺ＡＥ上の点Ｏを通る平面の名称を答えなさい。

　　　　≪答≫　二等辺三角形

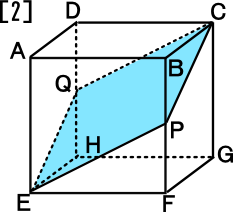
$立方体の切り口$

［２］　２点Ｃ，Ｅと辺ＢＦの中点Ｐ、辺ＤＨの中点Ｑを通る平面の名称を答え
　　　なさい。

　　　　≪答≫　ひし形

【練習問題２】
右図の［１］［２］は、１辺が１２ｃｍの立方体です。
以下の問いに答えなさい。

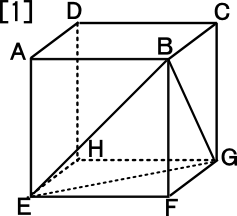
$切り取った立方体の体積$

［１］　右図のように、立方体を、３点Ｂ，Ｅ，Ｇを通る平面で２つに分ける。
　　　このとき、点Ｄをふくむ側の立体の体積を答えなさい。

　　　≪立方体の体積≫
　　　　　１２×１２×１２
　　　　＝１７２８

　　　≪三角すいＢＦＥＧの体積≫
　　　　　１３×｛（１２×１２÷２）×１２｝
　　　　＝２８８

　　　≪立方体－三角すいの体積≫
　　　　　１７２８－２８８
　　　　＝１４４０

　　　　≪答≫　体積：１４４０ｃｍ³

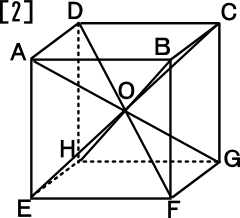
$切り取った立方体の体積$

［２］　右図のように、立方体に対角線を引き、対角線の交点をＯとする。
　　　このとき、底面をＥＦＧＨ、頂点をＯとする立体の面積を求めなさい。

　　　　　１３×｛（１２×１２）×６｝
　　　　＝２８８

　　　　≪答≫　体積：２８８ｃｍ³

【練習問題３】
右図の［１］［２］は、１辺が１２ｃｍの立方体です。
以下の問いに答えなさい。
（ちょっと難しいけど気付けば簡単！）

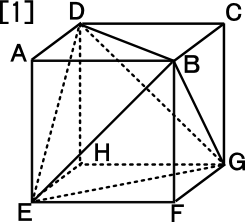
$切り取った立方体の体積$

［１］　右図の４点ＢＤＥＧを頂点とする立体の体積を求めなさい。

　　　≪立方体の体積≫
　　　　　１２×１２×１２
　　　　＝１７２８

　　　≪三角すいＥＡＢＤの体積≫
　　　　　１３×｛（１２×１２÷２）×１２｝
　　　　＝２８８

　　　※同じ形が全部で４個（ＥＡＢＤ、ＢＦＧＥ、ＧＣＢＤ、ＤＨＥＧ）
　　　　　２８８×４
　　　　＝１１５２

　　　≪立方体の体積－三角すい４つのの体積≫
　　　　　１７２８－１１５２
　　　　＝５７６

　　　　≪答≫　体積：５７６ｃｍ³

$切り取った立方体の体積$

［２］　右の立方体を、２点Ｆ，Ｈと、辺ＢＣ上の点Ｐ、辺ＣＤの点Ｑを通る
　　　平面で２つに分ける。（ＣＰ＝ＣＱ＝４ｃｍ）
　　　このとき、点Ｇをふくむ側の立体の体積を答えなさい。

　　　≪ｘを求める≫
　　　　　ｘ：（ｘ＋１２）　＝　４：１２　
　　　　１２ｘ＝４（ｘ＋１２）
　　　　ｘ＝６

　　　≪三角すいＲＧＦＨの体積≫
　　　　　１３×｛（１２×１２÷２）×（６＋１２）｝
　　　　＝４３２

　　　≪三角すいＲＣＰＱの体積≫
　　　　　１３×｛（４×４÷２）×６｝
　　　　＝１６

　　　≪三角すいＲＧＦＨの体積－三角すいＲＣＰＱの体積≫
　　　　　４３２－１６
　　　　＝４１６

　　　　≪答≫　体積：４１６ｃｍ³