中学３年数学練習問題　三平方の定理/定期テスト対策問題

ＴＯＰ
＞
中学３年　数学　練習問題一覧
＞
『第７章　三平方の定理』の復習テスト

勉強しないで後悔するくらいなら、
後悔してもいいから、勉強しよう。
勉強すれば、必ず力になる。
勉強すれば、必ず自分のためになる。
勉強すれば、後悔なんてしない。

～　中学３年　数学　～

『第７章　三平方の定理』の復習テスト

第７章　三平方の定理

＜前：『第７章　三平方の定理』の復習テストの問題　　Ｌ４６- 標本調査の問題：次＞

$三平方の定理$

【練習問題１】　　（参照　：　Lesson41　Lesson42 ）
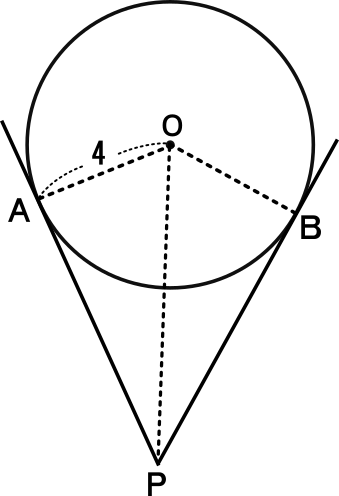
右図の円Ｏは半径４ｃｍの円である。
この円Ｏに２本の接線をひき、円との接点をそれぞれ点Ａ，Ｂとし、接線の交点を点Ｐとする。
四角形ＯＡＰＢの面積が３２ｃｍ²のとき、ＯＰの長さを求めなさい。

　＜△ＡＯＰの面積を求める＞
　　△ＡＯＰ＝△ＢＯＰなので、
　　△ＡＯＰ＝３２÷２＝１６（ｃｍ²）

　＜△ＡＰの長さを求める＞
　　ＡＰ×４÷２＝１６
　　ＡＰ＝８（ｃｍ）

　＜ＯＰの長さを求める＞
　　ＯＰ²＝４²＋８²
　　ＯＰ²＝８０

　　ＯＰ＝± $平方根$ ８０
　　　　＝±４ $平方根$ ５

　　ＯＰ＞０なので、
　　ＯＰ＝４ $平方根$ ５

　　≪答≫　４ $平方根$ ５ｃｍ

$三平方の定理$

【練習問題２】　　（参照　：　Lesson41　Lesson42 ）
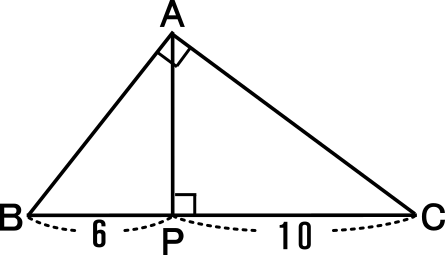
右図の直角三角形ＡＢＣで、点ＡからＢＣに垂線をひき、ＢＣとの交点を点Ｐとする。
このとき以下の質問に答えなさい。
　　※長さの単位はｃｍとする

［１］　ＡＣの長さを求めなさい。

　　△ＡＢＣと△ＰＡＣにおいて、
　　∠ＢＡＣ＝ＡＰＣ＝９０°　・・・①
　　∠Ｃ＝∠Ｃ　・・・②
　　①，②より
　　△ＡＢＣ∽ＰＡＣ

　＜ＡＣを相似比を使って求める＞
　　ＢＣ：ＡＣ＝ＡＣ：ＰＣなので、
　　１６：ＡＣ＝ＡＣ：１０
　　（ＡＣ）²＝１６０
　　ＡＣ＝± $平方根$ １６０
　　　　＝±４ $平方根$ １０

　　ＡＣ＞０なので、
　　ＡＣ＝４ $平方根$ １０

　　≪答≫　４ $平方根$ １０ｃｍ

［２］　ＡＰの長さを求めなさい。

　　△ＰＡＣにおいて、
　　ＡＰ²＋１０²＝（４ $平方根$ １０）²
　　ＡＰ²＝６０

　　ＡＰ＝± $平方根$ ６０
　　　　＝±２ $平方根$ １５

　　ＡＰ＞０なので、
　　ＡＰ＝２ $平方根$ １５

　　≪答≫　２ $平方根$ １５ｃｍ

$三平方の定理$

【練習問題３】　　（参照　：　Lesson41　Lesson42　Lesson43 ）
右図の△ＡＢＣの各座標はＡ（－２，４），Ｂ（－７，－８），Ｃ（２，－２）である。
このとき以下の質問に答えなさい。

［１］　ＡＢ，ＢＣ，ＣＡの長さをそれぞれ求めなさい。

　＜ＡＢの長さを求める＞
　　　 $平方根$ ｛－２－（－７）｝²＋｛４－（－８）｝²
　　＝ $平方根$ ２５＋１４４
　　＝ $平方根$ １６９
　　＝１３

　＜ＢＣの長さを求める＞
　　　 $平方根$ （－７－２）²＋｛－８－（－２）｝²
　　＝ $平方根$ ８１＋３６
　　＝ $平方根$ １１７
　　＝３ $平方根$ １３

　＜ＣＡの長さを求める＞
　　　 $平方根$ ｛２－（－２）｝²＋（－２－４）²
　　＝ $平方根$ １６＋３６
　　＝ $平方根$ ５２
　　＝２ $平方根$ １３

　　≪答≫　ＡＢ：１３，　ＢＣ：３ $平方根$ １３，　ＣＡ：２ $平方根$ １３

［２］　△ＡＢＣはどのような三角形か答えなさい。

　　ＢＣ²＋ＣＡ²＝ＡＢ²にあてはめてみる
　　（３ $平方根$ １３）²＋（２ $平方根$ １３）²＝１３²
　　１１７＋５２＝１６９
　　１６９＝１６９

　　ＢＣ²＋ＣＡ²＝ＡＢ²が成り立つので、
　　△ＡＢＣは直角三角形である

　　≪答≫　直角三角形

［３］　△ＡＢＣの面積を求めなさい。

　　　３ $平方根$ １３×２ $平方根$ １３÷２
　　＝３９

　　≪答≫　３９

$三平方の定理$

【練習問題４】　　（参照　：　Lesson41　Lesson42 ）
右図の△ＡＢＣの面積を求めなさい。
　　※長さの単位はｃｍとする

　　点Ａから辺ＢＣに垂線をひき、交点を点Ｐ，ＢＰをｘｃｍとする

　＜２つの三角形について、三平方の定理を利用して表す＞
　　△ＡＢＰは、
　　ＡＰ²＋ｘ²＝８²
　　ＡＰ²＝８²－ｘ²

　　△ＡＣＰは、
　　ＡＰ²＋（１２－ｘ）²＝１０²
　　ＡＰ²＝１０²－（１２－ｘ）²

　＜ＡＰ²について以下が成り立つ＞
　　８²－ｘ²＝１０²－（１２－ｘ）²

　　上の式を展開すると、
　　６４－ｘ²＝１００－（１４４－２４ｘ＋ｘ²）
　　６４－ｘ²＝１００－１４４＋２４ｘ－ｘ²
　　２４ｘ＝１０８
　　　　ｘ＝９２

　＜ＡＰの値を求める＞
　　ＡＰ²＝８²－ｘ²にｘ＝９２を代入する
　　ＡＰ²＝８²－（９２）²
　　　　　＝６４－８１４
　　　　　＝１７５４

　　ＡＰ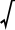＝ $平方根$ １７５４
　　　　＝５ $平方根$ ７２

　＜△ＡＢＣの面積を求める＞
　　　１２×５ $平方根$ ７２÷２
　　＝１５ $平方根$ ７

　　≪答≫　１５ $平方根$ ７ｃｍ²

$三平方の定理$

【練習問題５】　　（参照　：　Lesson41　Lesson42　Lesson44　Lesson45 ）
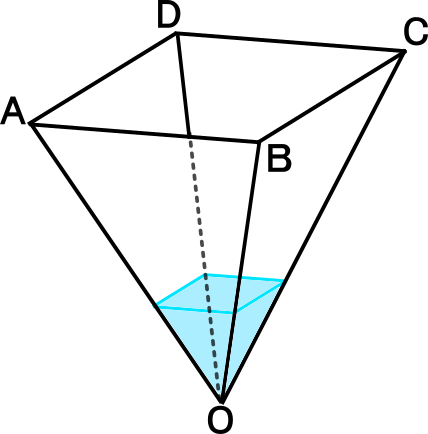
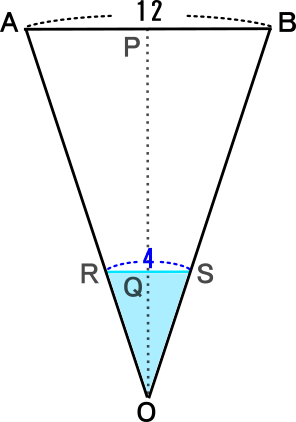
右図は、底面の正方形１辺の長さが１２ｃｍで、容量が８６４ｍｌの正四角すいＯＡＢＣＤの容器を水平に置き、そこに水を入れたものである。
このとき以下の質問に答えなさい。

［１］　ＡＯの長さを求めなさい。

　　辺ＡＢ側から側面を真横から見ると、右の下図のようになる

　＜容器の高さ（ＰＯ）を求める＞
　　容器の高さをｘｃｍとする
　　１２×１２×ｘ÷３＝８６４（ｍｌ）
　　ｘ＝１８（ｃｍ）
　　★容器の高さは、１８ｃｍ

$三平方の定理$

　＜ＡＯの長さを求める＞
　　ＡＰ＝６ｃｍ，ＰＯ＝１８ｃｍなので、
　　ＡＯ²＝６²＋１８²
　　　　　＝３６０

　　ＡＯ＝± $平方根$ ３６０
　　　　＝±６ $平方根$ １０

　　ＡＯ＞０なので、
　　ＡＯ＝６ $平方根$ １０

　　≪答≫　６ $平方根$ １０ｃｍ

［２］　水面の１辺が４ｃｍのとき、水が入っていない部分の容量を求めなさい。

　＜ＱＯの長さを求める＞
　　ＲＳ：ＡＢ＝ＱＯ：ＰＯなので、
　　４：１２＝ＱＯ：１８
　　ＱＯ＝６（ｃｍ）

　＜水の部分の容量を求める＞
　　４×４×６÷３＝３２（ｍｌ）

　＜水の入っていない部分の容量を求める＞
　　８６４－３２＝８３２（ｍｌ）

　　≪答≫　８３２ｍｌ

$三平方の定理$

【練習問題６】　　（参照　：　Lesson41　Lesson42　Lesson44　Lesson45 ）
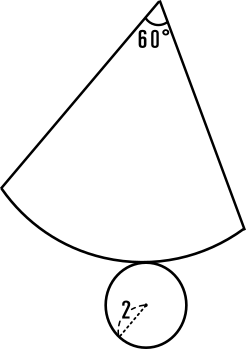
右図の円すいの展開図について、以下の質問に答えなさい。
　　※長さの単位はｃｍとする

［１］　母線の長さを求めなさい。

　＜おうぎ形の弧の長さを求める＞
　　おうぎ形の弧の長さ＝底面の円周なので、
　　２π×２＝４π（ｃｍ）

　＜母線（おうぎ形の半径）を求める＞
　　母線をｒｃｍとすると、
　　２πｒ×６０３６０＝４π（ｃｍ）
　　ｒ＝１２（ｃｍ）

　　≪答≫　１２ｃｍ

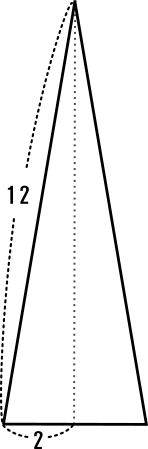
$三平方の定理$

［２］　円すいの体積を求めなさい。

　　展開図を組み立てると、右の下図ような円すいになる

　＜円すいの高さを求める＞
　　三平方の定理より、
　　２²＋高さ²＝１２²
　　高さ²＝１４０

　　高さ＝± $平方根$ １４０
　　　　＝±２ $平方根$ ３５

　　高さ＞０なので、
　　高さ＝２ $平方根$ ３５（ｃｍ）

　＜円すいの体積を求める＞
　　　π×２²×２ $平方根$ ３５÷３
　　＝８ $平方根$ ３５３π

　　≪答≫　８ $平方根$ ３５３π ｃｍ³

$三平方の定理$

【練習問題７】　　（参照　：　Lesson41　Lesson42　Lesson44　Lesson45 ）
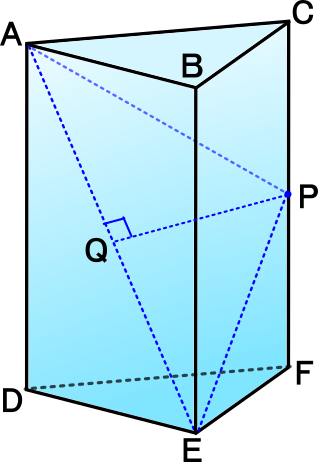
右図の正三角柱は底面の正三角形の１辺の長さが４ｃｍで、表面積は７２ $平方根$ ３ｃｍ²である。
このとき以下の質問に答えなさい。

［１］　底面の面積を求めなさい。

　＜底面の正三角形の高さを求める＞
　　三平方の定理より、
　　２²＋高さ²＝４²
　　高さ²＝１２

　　高さ＝± $平方根$ １２
　　　　＝±２ $平方根$ ３

　　高さ＞０なので、
　　高さ＝２ $平方根$ ３（ｃｍ）

　＜底面の正三角形の面積を求める＞
　　４×２ $平方根$ ３÷２＝４ $平方根$ ３（ｃｍ²）

　　≪答≫　４ $平方根$ ３ｃｍ²

［２］　正三角柱の体積を求めなさい。

　＜側面積の四角形１枚の面積を求める＞
　　７２ $平方根$ ３－（２×４ $平方根$ ３）＝６４ $平方根$ ３（ｃｍ²）
　　６４ $平方根$ ３÷４＝１６ $平方根$ ３（ｃｍ²）

　　★四角形１枚の面積は、１６ $平方根$ ３ｃｍ²

　＜側面積の四角形の縦（＝正三角柱の高さ）の長さを求める＞
　　四角形の縦をｘｃｍとする
　　４×x＝１６ $平方根$ ３
　　x＝４ $平方根$ ３（ｃｍ）

　　★正三角柱の高さは、４ $平方根$ ３ｃｍ

　＜正三角柱の体積を求める＞
　　４ $平方根$ ３×４ $平方根$ ３＝４８（ｃｍ³）

　　★正三角柱の体積は、４８ｃｍ³

　　≪答≫　４８ｃｍ³

［３］　点Ｐを辺ＣＦの中点としたとき、△ＡＰＥの面積を求めなさい。

　＜ＡＥの長さを求める＞
　　ＡＥ²＝４²＋（４ $平方根$ ３）²
　　　　　＝６４

　　ＡＥ＝±８

　　ＡＥ＞０なので、
　　ＡＥ＝８（ｃｍ）

　＜ＡＰ（＝ＥＰ）の長さを求める＞
　　ＣＰ＝４ $平方根$ ３÷２
　　　　＝２ $平方根$ ３

　　ＡＰ²＝４²＋（２ $平方根$ ３）²
　　　　　＝２８

　　ＡＰ＝± $平方根$ ２８
　　　　＝±２ $平方根$ ７

　　ＡＰ＞０なので、
　　ＡＰ＝２ $平方根$ ７（ｃｍ）

　＜△ＡＰＥの高さを求める＞
　　△ＡＰＥの高さをＰＱとする

　　ＰＱ²＋ＡＱ²＝ＡＰ²なので、
　　ＰＱ²＋４²＝（２ $平方根$ ７）²
　　ＰＱ²＝１２

　　ＰＱ＝± $平方根$ １２
　　　　＝±２ $平方根$ ３

　　ＰＱ＞０なので、
　　ＰＱ＝２ $平方根$ ３（ｃｍ）

　＜△ＡＰＥの面積を求める＞
　　８×２ $平方根$ ３÷２＝８ $平方根$ ３（ｃｍ²）

　　≪答≫　８ $平方根$ ３ｃｍ²

＜前：『第７章　三平方の定理』の復習テストの問題　　Ｌ４６- 標本調査の問題：次＞

中１数学・練習問題一覧中２数学・練習問題一覧中３数学・練習問題一覧

当サイトでご紹介している
教育系サイト

家庭教師のガンバ

家庭教師のガンバは、勉強が嫌いな子、勉強が苦手な子、勉強のやり方がわからない子を中心に２０年以上運営されている家庭教師センターです。

生徒やご家庭の状況や希望に合わせてやり方を相談して決めてくれます。

母子家庭に優しい優遇プランもあって、教育費にどうしても費用をかけられないご家庭にもピッタリ。

【派遣地域】
東京・神奈川・埼玉・千葉・茨城

【詳細】

家庭教師のがんば

家庭教師のガンバ

中学生　勉強なんて　怖くない

ＭＥＮＵ